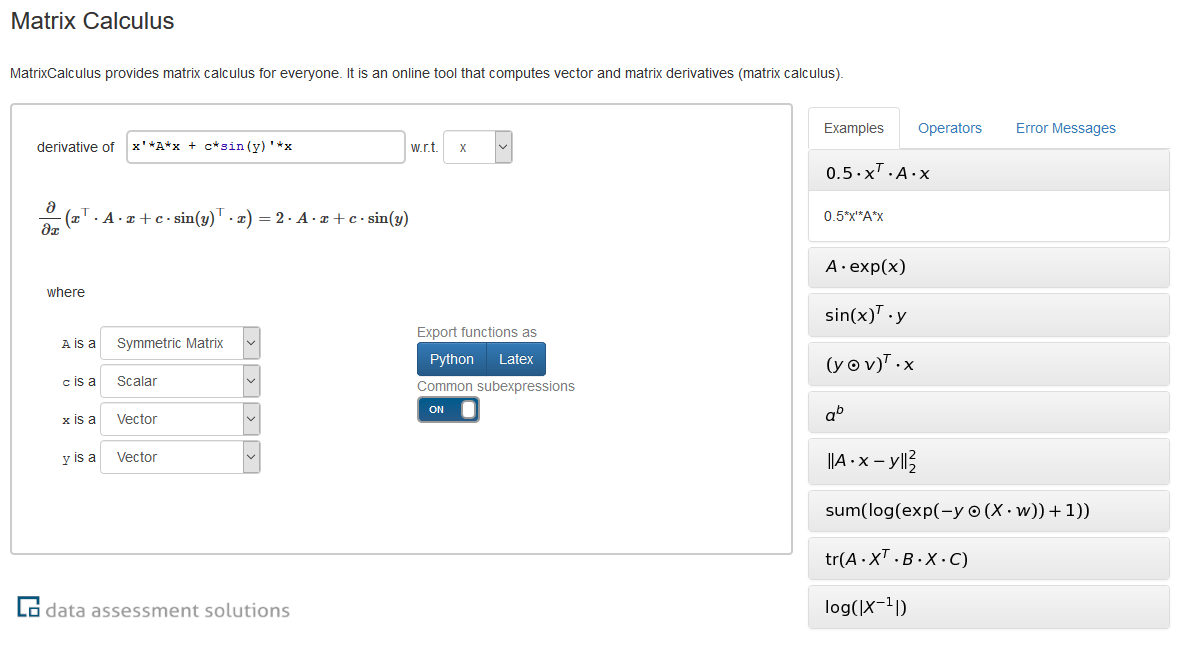
Matrix calculus: Eine kleine Applikation mit großer Wirkung
Die Applikation www.matrixcalculus.org wurde im letzten Jahr über 30.000-mal genutzt. Die meisten Nutzer kommen aus weltweit führenden Universitäten und den AI Abteilungen großer Internetkonzerne wie Google Deepmind und Facebook. Ihren Durchbruch hatte die Applikation am 18. November 2017 als sie in den Hackernews des Startup Inkubators Y Combinator auf Platz 1 gelistet war. Allein an diesem Tag wurde die Seite mehr als 12.000-mal besucht. In diesem Artikel erklären wir, was Matrix Calculus ist und warum diese Applikation so erfolgreich ist.
Doch zunächst ein historischer Exkurs:
Die Analysis, also Regeln zum Differenzieren (Ableiten) und Integrieren von Funktionen, wurde vor mehr als 350 Jahren von Isaac Newton und Gottfried Wilhem Leibniz in Hannover (unserem Firmensitz) entwickelt. Matrixalgebra bzw. Lineare Algebra, die unter anderem zum Lösen linearer Gleichungssysteme verwendet wird, wurde vor ca. 150 Jahren von Hermann Grassmann, James Joseph Sylvester und Arthur Cayley entwickelt. Als Matrix Calculus bezeichnet man das Problem, die Ableitung einer als Matrixalgebraausdruck gegebenen Funktion wieder als Matrixalgebraausdruck anzugeben.
Matrix Calculus ist ein interessantes Problem, da Matrixalgebraausdrücke auf modernen Computern sehr schnell ausgewertet werden können. Viele Optimierungsprobleme aus dem maschinellen Lernen lassen sich durch Matrixalgebraausdrücke beschreiben. Effiziente Algorithmen zum Lösen dieser Probleme benötigen auch Ableitungen dieser Ausdrücke, z.B. deren Gradienten. Mit Hilfe eines Matrix Calculus lassen sich Gradienten und auch Ableitungen höherer Ordnung sehr effizient auswerten, was zu einer Beschleunigung der Optimierungsalgorithmen führt.
Obwohl die Regeln des Ableitens und die Sprache der Matrixalgebra schon weit über hundert Jahre alt sind, war das Matrix Calculus Problem bis vor Kurzem noch ungelöst. Bislang wurden bekannte händisch oder halbautomatisch berechnete Ableitungen in einem Matrix Cookbook tabelliert. An der Universität Jena wurde jetzt ein rein automatischer Matrix Calculus Algorithmus entwickelt, der als Applikation unter www.matrixcalculus.org zur Verfügung steht. Wer einmal selber die Ableitung eines Matrixalgebraausdrucks von Hand versucht hat, wird die Begeisterung der AI-Forschungs-Community über dieses lang ersehnte Tool verstehen.
Der Kern des Matrix Calculus Problems ist, dass Matrixalgebra keine gute Sprache ist, um Analysis zu betreiben. Tensoren, die Matrizen verallgemeinern, aber mit Hilfe von Indizes niedergeschrieben werden müssen, eignen sich viel besser für die Analysis. Die Lösung des Matrix Calculus Problems war also die Übersetzung von Matrixalgebraausdrücken in Tensorausdrücke, die einfach abgeleitet werden können. Da man aber am Ende, wenn möglich, wieder Matrixalgebraausdrücke haben will, bleibt noch das Problem, Tensorausdrücke in Matrixalgebraausdrücke zu übersetzen. Dieses Problem ist allerdings viel schwieriger als die Übersetzung in die andere Richtung. Die realisierte Lösung ist regelbasiert und verwendet mehrere hundert Regeln. Das Regelsystem wurde in einem längeren, iterativen Prozess korrekt und vollständig gemacht. Die in diesem Prozess verwendeten Visualisierungen wurden an der Universität Jena in Zusammenarbeit mit DAS Research entwickelt.
Veröffentlichung: J. Giesen, J. Klaus, S. Laue und F. Schreck. Visualization Support for Developing a Matrix Calculus Algorithm: A Case Study. Proceedings of the 21st EG/VGTC Conference on Visualization (EUROVIS), (2019)
