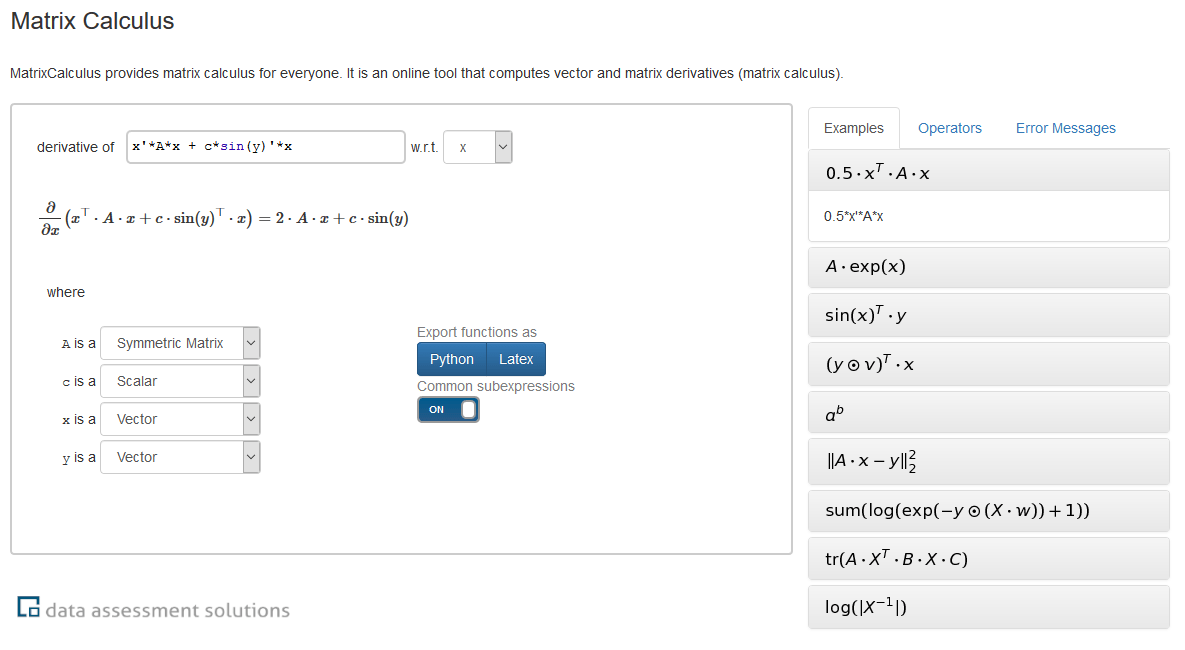
Matrix calculus: A small tool with a big impact
The application www.matrixcalculus.org was used over 30,000 times last year. Most users come from the world leading universities and the AI departments of major Internet companies such as Google Deepmind and Facebook. The application had its breakthrough on November 18, 2017 when it was ranked #1 in the hacker news of the startup incubator Y Combinator. On this day alone, the site was visited more than 12,000 times. In this article we explain what Matrix Calculus is and why this application is so successful.
But first a historical excursion:
Analysis, i.e. rules for differentiating (deriving) and integrating functions, was developed more than 350 years ago by Isaac Newton and Gottfried Wilhem Leibniz in Hanover (our company headquarters). Matrix algebra or linear algebra, which is used for solving linear systems of equations, was developed about 150 years ago by Hermann Grassmann, James Joseph Sylvester and Arthur Cayley. Matrix Calculus is the term used to describe the problem of specifying the derivation of a function given as a matrix algebra expression as a matrix algebra expression again.
Matrix Calculus is an interesting problem because matrix algebra expressions can be evaluated very quickly on modern computers. Many optimization problems from machine learning can be described by matrix algebra expressions. Efficient algorithms for solving these problems also require derivatives of these expressions, e.g. their gradients. With the help of a Matrix Calculus, gradients and derivatives of higher order can be evaluated very efficiently, which leads to an acceleration of the optimization algorithms.
Although the rules of derivation and the language of matrix algebra are well over a hundred years old, the Matrix Calculus problem was unsolved until recently. So far, known manually or semi-automatically calculated derivatives have been tabulated in a Matrix Cookbook. At the University of Jena, a purely automatic Matrix Calculus algorithm has now been developed, which is available online at www.matrixcalculus.org. Anyone who has ever tried to derive a matrix algebra expression by hand will understand the enthusiasm of the AI research community for this long-awaited tool.
The core of the Matrix Calculus problem is that matrix algebra is not a good language to use for analysis. Tensors that generalize matrices but must be written down with the help of indices are much better suited for analysis. So the solution to the Matrix Calculus problem was to translate matrix algebra expressions into tensor expressions whose derivatives can be easily computed. However, since one wants a matrix algebra expression again in the end, if possible, one needs to translate tensor expressions into matrix algebra expressions. This problem is much more difficult than the translation in the other direction. The implemented solution is rule-based and uses several hundred rules. The rule based system was made correct and complete in an iterative process. The visualizations used in this process were developed at the University of Jena in cooperation with DAS Research.
Publication: J. Giesen, J. Klaus, S. Laue und F. Schreck. Visualization Support for Developing a Matrix Calculus Algorithm: A Case Study. Proceedings of the 21st EG/VGTC Conference on Visualization (EUROVIS), (2019)
