The efficient solution of optimization problems is a central task in machine learning and in the larger field of data science. Therefore, we are developing GENO (generic optimization), a domain-specific language (DSL) for generating solution software for various optimization problems from simple specifications. An important component of GENO is a matrix calculus for computing symbolic derivatives of mathematical expressions.

Building on the matrix calculus, we have now developed an algorithm for certifying the convexity of optimization problems. For convex optimization problems, all local optima are also global optima. The information whether a problem is convex or not is of interest because the solution software generated by GENO always computes a global optimum only for convex problems. For non-convex problems, a local optimum is computed, of which it is impossible to say how much worse it is than the global optimum.

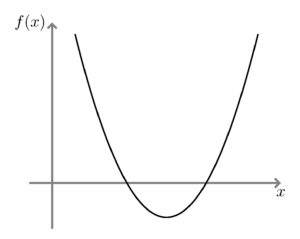
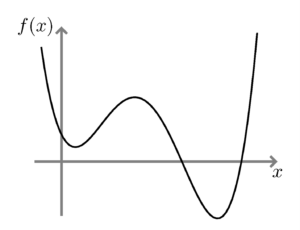
Left: A convex function with easy-to-compute global minimum. Right: A non-convex function with two local minima. In general, a global minimum of a non-convex function is not easy to compute.

However, the new algorithm is not only interesting for GENO. With the help of the algorithm, we were able to certify new classes of functions as convex, which can now be used in applications.

Publication: J. Klaus, N. Merk, K. Wiedom, S. Laue and J. Giesen. Convexity Certificates from Hessians. Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022).