Ein Optimierungsproblem ist durch seine Variablen, seine Zielfunktion und Nebenbedingungen gegeben. Gesucht wird eine Belegung der Variablen mit Werten, so dass der Wert der Zielfunktion optimiert wird und alle Nebenbedingungen erfüllt werden.

Bei Data Assessment Solutions modellieren wir viele Aufgaben als Optimierungsproblem. Betrachten wir zum Beispiel eine einfache Projektplanungsaufgabe. Dabei sei x(i,j,k) die Variable der Stunden, die der Consultant i am Tag j auf dem Projekt k verbringt.  Dann ist eine Nebenbedingung, dass die Summe über alle Projekte k für den Consultant i am Tag j nicht mehr als zehn Stunden sein darf. Eine mögliche Zielfunktion ist die Maximierung der verrechenbaren Stunden aller Consultants in einem gegebenen Zeitraum.

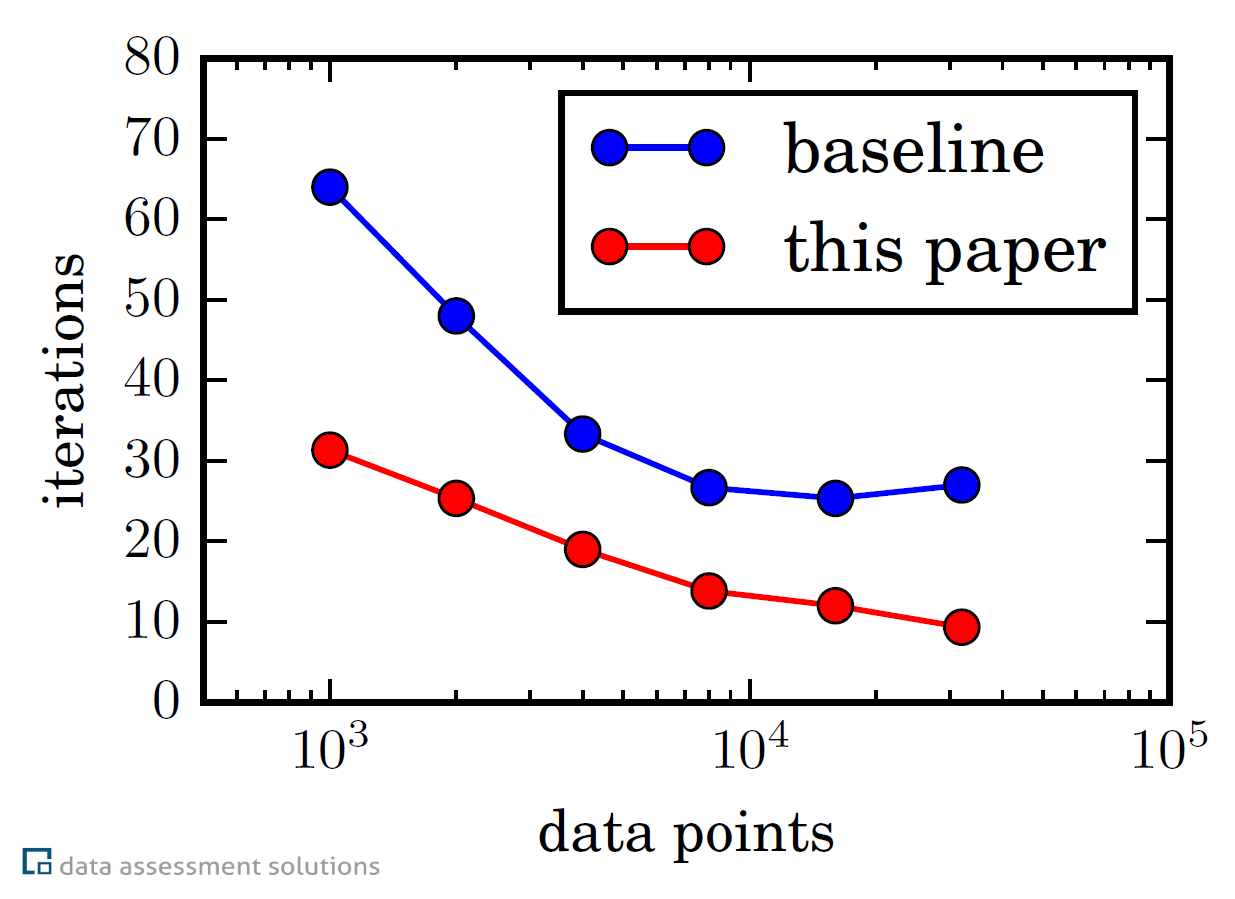
Sören Laue und Joachim Giesen von DAS Research haben einen neuen Algorithmus zur Lösung von Optimierungsproblemen mit vielen Nebenbedingungen entwickelt, der verteilte Prozessoren in einem Computercluster oder die vielen Rechenkerne moderner CPUs ausnutzt. Zuerst würde man annehmen, dass jeder verteilte Algorithmus zur Lösung von Optimierungsproblemen mit Nebenbedingungen drei ineinander geschachtelte Schleifen benötigt: Eine innere Schleife zur Lösung von Optimierungsproblemen ohne Nebenbedingungen, eine Schleife zur Erfüllung der Nebenbedingungen, und eine äußere Schleife zur Erreichung eines Konsens der auf verschiedenen Computern oder Rechenkernen vorliegenden Lösungen. Sören Laue und Joachim Giesen konnten zeigen, dass nur zwei geschachtelte Schleifen ausreichen, was zu einer signifikanten Beschleunigung des verteilten Algorithmus führt.

Veröffentlichung: J. Giesen und S. Laue. Combining ADMM and the Augmented Lagrangian Method for Efficiently Handling Many Constraints. Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI), (2019)